Physics of Gas-Liquid Chromatography

Introduction

Today the modeling of GC retention is confined to G=H-TS Gibbs type equations. From a practical point of view, which is common in the chromatographic lab, column polarity or boiling point cannot be described by this Gibbs equation. Vapor liquid equilibria apply much better to gas chromatography. However, polymer phases have infinite molar mass so molar mass is not defined, impairing application of Henry’s law to GC. Hence thermodynamic theory of GC has continued to model GC as if it were a steam engine. In this blog Vapor-Liquid Equilibrium theory will be applied to GLC. The polymer problem is solvable, but that problem will not be solved here…

1.Physical properties

Peak retention time is a result of equilibrium partition over gas and liquid phase and carrier velocity. Vapor-liquid phase diagrams of binary mixtures obey Henry’s law¹ :
       Henry’s law [Pa]

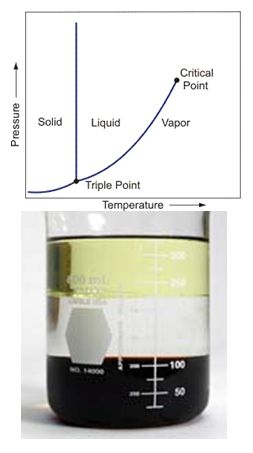Pure liquid vapor pressure Pⁱ is the boundary between the liquid phase and gas phase. Traditionally, Pⁱ is calculated using the van der Waals Equation Of State using the critical point. Another equation is the Antoine equation. Both EOS and Antoine apply 3 or 4 parameters that are fitted on measured values. Most Pⁱ measurements were performed before 1947 [2].
Mixing behavior of a component i in stationary phase L is accounted for by the activity coefficient γ_i^L, a measure of stationary phase repulsion of molecule i. This property is referred to as column polarity or column selectivity by chromatographers. A rule of thumb is that stationary phase polarity and analyte polarity should match² . The challenge to understand mixing and demixing from polarity alone may become clear looking at a beaker with a 3 layer system. When stirred, an emulsion forms, but when allowed to settle these layers return, densest at the bottom. Demixing is caused by elevated values of the activity coefficient.
Henry’s law description of the partition of an analyte i over the gas phase and liquid phase is the ratio of mole fractions in the vapor phase (γ_i) and the liquid phase (x_i):
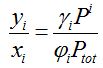       volatility [-]

Fugacity coefficient φ_i is a measure for deviation from ideal gas law. The activity coefficient equals one in a pure liquid or γ_iⁱ = 1, whereas pure vapor fugacity coefficient φ_i is not. Daltons’s law states the gas law would hold³ for vapor molecules and φ_i =1. Hence follows:

             VLE                             [-]

Ideal binary mixtures like Benzene (1) Toluene (2) have activity coefficients γ₁²= γ₂¹ = 1 .Total pressure P_tot is related with volume V_G containing total amount n^G [mole] of carrier gas at temperature T by ideal gas law:

         ideal gas law                [J]

This law applies to carrier gases below 30 bar. Molar volume is out of fashion today but between 1900 and 1940 it was a popular concept. Liquid molar volume V ^L, used today in activity coefficient equations, is defined with molar mass M ^L and density ρ^L :

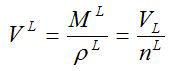        liquid molar volume    [mL/mol]

Molar volume V ^L divided by the Avogadro number is supposed to equal molecular volume, assuming free intermolecular volume can be neglected in liquids. Note that molar mass times moles is mass: n^LM ^L = m_L.
Gas molar volume V ^G is defined with gas volume V_G and ideal gas law:

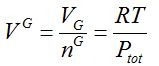               gas molar volume        [mL/mol]

Unclear PV=RT statements arise from this molar gas volume!

2.Phase ratio of GLC retention time

The volume ratio of stationary phase V_L to mobile phase V_G can be derived from capillary inner diameter d_c and liquid film thickness d_f using the cylinder volume equation:

                   phase ratio       [-]

Phase ratio β is independent of column length L. Temperature may change β in case of different thermal expansion of fused silica to change d_c and the stationary phase polymer to change d_f . However, β is always assumed to be temperature independent.

3.GLC retention time

Assuming equilibrium between gas phase and liquid phase is justified by the small size of chromatographic wall coated open tube (WCOT) columns (50µm < d_c < 1000µm).

Peak retention time then follows from equilibrium partition over gas phase and liquid phase of molecules in a capillary.

In the picture a capacity factor k_i=3 is shown. Capacity factor k_i is the ratio of residence times in the mobile phase t₀ and the stationary phase t_i–t₀ which equals the ratio of the number of mol(ecul)es in the stationary phase to the number of mol(ecul)es in the mobile phase:

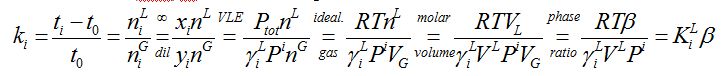   [-]        (1)

This result was also reported in 1958 [4].

Unknown properties are: component i activity coefficient in stationary phase γ_i^L and polymer molar volume V ^L. Packed column retention volume has been used from the onset of liquid chromatography by Tswett[1]. Net retention volume V_i^G0 is retention t_i per gram m_L of stationary phase and involves flow measured with a bubble flow meter at temperature T_atm and pressure P_atm of the lab [3]:

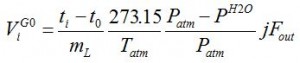             retention volume          [mL/g]

Pure liquid water vapor pressure P ^H2O is subtracted from the column outlet flow.

Outlet gas flow is corrected to average flow F̄ by the James and Martin j relation:

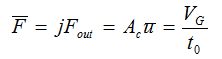                    average flow                [mL/min]

Using average velocity ū=L/t₀ and A_c is cross section inner area of the column.

Omitting the atmospheric bubble flow meter corrections of P and T in retention volume:

       [mL/g]              (2)

Summarizing, we have for capillary GC:

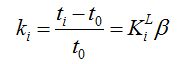         capacity factor                         [-]

And for packed column GC:

           retention volume          [mL/g]

Where the equilibrium “constant” depends on temperature and stationary phase:

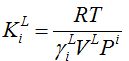                LG equilibrium                        [-]

In hindsight, V_o^G never became the standard and the packed column technology only occupies one page in Vapor-Liquid Equilibrium modeling of today (see Flory Huggins [1]).

Equilibrium constant K_i^L relates component i concentrations in liquid and gas (C_i^G = K_i^LC_i^L). Some researchers considered this to be Henry’s law.

Activity coefficient γ_i^L of component i in stationary phase L is the only unknown property.

Molar mass is infinite for polymers, but packed columns may have a well defined M ^L.

Kovats index is the standard by ASTM temperature programmed GC method (ASTM D6729, D6730 & D6733) today.

Retention volume relations to Vapor-Liquid Equilibrium (VLE) thermodynamics have been researched since the 60’s. Introduction of standard pressure and the standard temperature of 0°C to retention volume caused non-standard, undocumented features leading to confusion and ambivalent values. Critique [5] on these pressure and temperature corrections is that they led to incomparable numbers for similar GLC analyses. Finally, this research went out of fashion [5] in the 80’s.

4.References

[1] R.C. Reid, J.M. Prausnitz, B.E. Poling (1987) The properties of Gases & Liquids ISBN 0-07-051799-1

[2] DANIEL R. STULL (1947) Vapor Pressure of Pure Substances: Organic Compounds, Ind. Eng. Chem. Vol. 39, No. 4 p.517-540.

[3] E. Díaz, A. Cazurro, S. Ordóñez, A. Vega and J. Coca (2007) DETERMINATION OF SOLUBILITY PARAMETERS AND THERMODYNAMIC PROPERTIES IN HYDROCARBON-SOLVENT SYSTEMS BY GAS CHROMATOGRAPHY Brazilian Journal of Chemical Engineering Vol. 24, No. 02, p.293 – 306.

[4] A.Kwantes and G.W.A Rijnders (1958) The determination of activity coefficients at infinite dilution by gas-liquid chromatography

[5] V. A. Davankov (2003) Critical reconsideration of the physical meaning and the use of fundamental retention parameters in gas chromatography. New IUPAC recommendations Chromatographia Vol 57, Supplement 1 (2003), S195-S198, DOI: 10.1007/BF02492102

___________________________________________

¹Which is the equality of liquid and gas fugacity (fiG = fiL).
²In case of analysis of green gasoline this rule cannot be obeyed because Ethanol is mixed with Hydrocarbons.
³Indirectly supported by the Poynting factor [1].
⁴Liquids have little volume variation with pressure or temperature compared to gases, so for gas chromatography retention volume is not very practical…